更高效的求幂运算
本文创建时间较早,已长时间未更新信息可能不准确,文章内容仅供参考。
描述
计算 x^n 常见的算法就是使用 n-1 次乘法自乘,更高效的做法我们可以使用递归。以乘法的次数来作为运行时间的度量,下面是两种算法的比较。
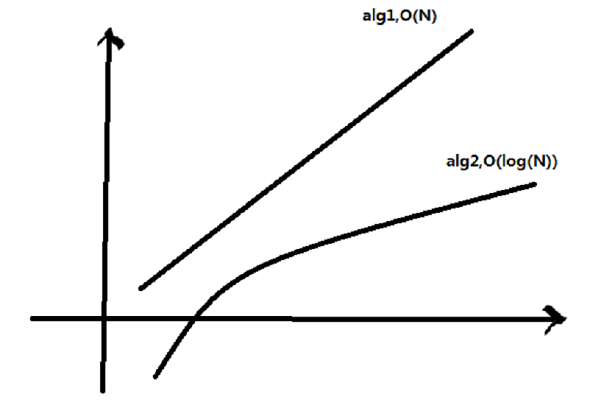
算法 2 的数学原理:
- 若 n 为偶数
X^n = X^(n/2) * X^(n/2). - 若 n 为基数
X^n = X^[(n-1)/2] * X^[(n-1)/2] * X.
实现
algorithm1
long pow1(int x, int n)
{
int i;
long res;
if(n == 0)
{
return 1;
}
res = x;
for(i = 1; i< n; i++)/*进行n-1次自乘运算*/
{
res *= x;
}
return res;
}
algorithm2
long pow2(long x, int n)
{
if(n == 0)
return 1;
if(n == 1)
return x;
if(x % 2 == 0)
return pow2(x * x, n / 2);
else
return pow2(x * x, n / 2) * x;
}
pow2(x * x, n / 2) => 幂运算 x^2 * x^(n/2),当 n 较大时,算法 2 的乘法运算次数明显减少。